Ứng dụng mô hình ARIMA dự báo xu hướng giá bạc thế giới
TS. Nguyễn Thị Thu Thủy
TS. Nguyễn Thị Thanh Loan
Email: nguyenthithanhloan@haui.edu.vn
TS. Đặng Thị Hồng Hà
Khoa Kế toán - Kiểm toán, Trường Kinh tế, Đại học Công nghiệp Hà Nội
Tóm tắt
Nghiên cứu tập trung vào việc ứng dụng mô hình ARIMA để dự báo xu hướng giá bạc thế giới với bộ dữ liệu trong giai đoạn 2021-2024 bằng phần mềm Stata. Kết quả nghiên cứu cho thấy dữ liệu giá bạc có tính dừng sau khi được thực hiện sai phân. Mô hình ARIMA đã được xây dựng phù hợp, đảm bảo các điều kiện về tính ổn định và khả nghịch, với các chỉ số đánh giá hiệu suất như: MAE và RMSE đạt giá trị rất nhỏ. Ngoài ra, nghiên cứu còn thực hiện so sánh kết quả với một số mô hình dự báo khác như: mô hình san mũ Holt-Winters, mô hình GARCH để đưa ra kết luận về việc sử dụng mô hình phù hợp cho dự báo giá bạc thế giới. Kết quả nghiên cứu cung cấp một công cụ để các nhà quản lý, nhà đầu tư nhận định được đúng về xu hướng biến động của thị trường, từ đó có các quyết định phù hợp.
Từ khoá: Dự báo, giá bạc, mô hình ARIMA, mô hình san mũ Holt-Winters, mô hình GARCH
Summary
This study focuses on applying the ARIMA model to forecast world silver price trends using data from 2021 to 2024, processed with Stata software. The research results indicate that the silver price data become stationary after differencing. The constructed ARIMA model meets the stability and invertibility conditions, with performance indicators such as MAE and RMSE showing very small values. In addition, the study compares the forecasting performance of ARIMA with other models, including the Holt-Winters exponential smoothing model and the GARCH model, to determine the most suitable approach for forecasting global silver prices. The findings provide a valuable tool for policymakers and investors to better understand market fluctuations and make more informed decisions.
Keywords: Forecast, silver price, ARIMA model, Holt-Winters exponential smoothing model, GARCH model
GIỚI THIỆU
Bạc là một trong những kim loại quý được giao dịch nhiều nhất trên thế giới, đóng vai trò quan trọng cả trong lĩnh vực tài chính và công nghiệp. Với mức tăng trưởng gần 92% trong 5 năm qua, bạc đã vượt qua cả vàng về tốc độ tăng trưởng và thu hút sự quan tâm lớn từ các nhà đầu tư. Theo dự báo của nhà giao dịch Bob Loukas, giá bạc có thể đạt mốc 50 USD/ounce trong tương lai nếu đà tăng tiếp tục. Với chính sách tiền tệ nới lỏng từ Cục Dự trữ Liên bang Mỹ (FED), việc cắt giảm lãi suất sẽ làm tăng sức hấp dẫn của bạc, đặc biệt khi các tài sản không sinh lãi như bạc được ưu tiên hơn trong bối cảnh lãi suất thấp (Thu Dung, 2024). Khác với vàng, bạc có một vai trò quan trọng trong công nghiệp, với ứng dụng rộng rãi trong các ngành sản xuất như: điện tử, năng lượng mặt trời và y tế. Sự kết hợp giữa tính chất tài chính và công nghiệp khiến bạc trở thành một trong những tài sản có tính biến động cao trên thị trường hàng hóa. Sự biến động giá bạc chịu ảnh hưởng của nhiều yếu tố kinh tế, tài chính và địa chính trị. Giá bạc có thể tăng hoặc giảm mạnh trong thời gian ngắn, phản ánh không chỉ sự thay đổi trong cung - cầu thực tế mà còn cả tâm lý đầu tư. Ví dụ, trong cuộc khủng hoảng tài chính toàn cầu năm 2008, giá bạc đã giảm mạnh do nhu cầu công nghiệp sụt giảm, nhưng sau đó phục hồi nhanh chóng nhờ vai trò trú ẩn an toàn. Do tính chất biến động này, việc nghiên cứu và dự báo giá bạc là một thách thức lớn nhưng cũng rất quan trọng đối với nhà đầu tư và các nhà hoạch định chính sách.
CƠ SỞ LÝ THUYẾT VÀ MÔ HÌNH NGHIÊN CỨU
Cơ sở lý thuyết
ARIMA là một trong những mô hình phổ biến nhất trong phân tích chuỗi thời gian. Mô hình này kết hợp 3 thành phần chính: Tự hồi quy (AR - AutoRegressive), Tích hợp (I - Integrated) và Trung bình trượt (MA - Moving Average). Ký hiệu là ARIMA(p, d, q).
Thành phần tự hồi quy (AR)
Đây là phần hồi quy tuyến tính biểu thị mối quan hệ giữa giá trị hiện tại của chuỗi thời gian và các giá trị quá khứ của nó. Thành phần này được biểu diễn bởi tham số p, là số bậc của phần tự hồi quy. Mô hình AR(p) của một chuỗi thời gian có thể được biểu diễn như sau:
Yt = c + ϕ1*Yt - 1 + ϕ2*Yt−2 +...+ ϕp*Yt - p + ϵt
Trong đó: c, ϕ1, ϕ2,..., ϕp là các hệ số hồi quy; ϵt là sai số ngẫu nhiên.
Thành phần tích hợp (I)
Thành phần này liên quan đến việc biến đổi chuỗi thời gian thành chuỗi không có xu hướng (stationary) bằng cách lấy sai phân (difference). Số lần lấy sai phân cần thiết để chuỗi trở nên không có xu hướng được biểu diễn bởi tham số d.
Thành phần trung bình trượt (MA)
Biểu thị mối quan hệ giữa giá trị hiện tại của chuỗi thời gian và giá trị sai số ngẫu nhiên của các dự đoán từ các bước trước đó (các giá trị nhiễu) để dự đoán giá trị hiện tại. Thành phần này được xác định bởi tham số q, là số bậc của phần trung bình trượt. Mô hình MA(q) của một chuỗi thời gian có thể được biểu diễn như sau:
Yt = μ + ϵt + θ1*ϵt−1 + θ2*ϵt−2 +...+ θq*ϵt - q
Trong đó: θ1, θ2,..., θq là các hệ số trung bình trượt; ϵt là sai số ngẫu nhiên.
Dữ liệu và mô hình nghiên cứu
Dữ liệu giá bạc thế giới được lấy từ trang web Investing.com (https://vn.investing.com/commodities/silver). Thời gian dữ liệu tải xuống từ trang web từ ngày 15/2/2021 đến 13/12/2024. Dữ liệu bao gồm 1.005 bản ghi (dòng), mỗi dòng là thông tin về một ngày giao dịch. Có 7 cột dữ liệu gồm: thời gian giao dịch, giá đóng cửa, giá mở cửa, giá cao nhất, giá thấp nhất, số lượng hợp đồng giao dịch trong ngày, mức thay đổi giá theo tỷ lệ phần trăm so với ngày trước đó.
Mô hình nghiên cứu sử dụng sự tích hợp của 2 quá trình: tự hồi quy bậc p - AR(p) và trung bình trượt bậc q - MA(q). Mô hình đầy đủ là ARIMA(p,d,q) với p là bậc tự hồi quy, d là bậc sai phân (số lần lấy sai phân) và q là bậc trung bình trượt.
Φp(B) (1 - B)d (Yt - µ) = θq(B) εt
Với Φp(B) = 1 - Φ1B - Φ2B2 - … - ΦpBp
Θp(B) = 1 + θ1B + θ1B2 + … + θqBq
Trong đó: B là hệ số độ trễ, theo đó BiYt = Yt-i và Bi εt = εt-i ; (1 - B)d là sai phân bậc d, µ phản ánh giá trị trung bình của Yt và εt là nhiễu trắng ở thời điểm t.
Phương pháp nghiên cứu
Nghiên cứu sử dụng cách tiếp cận theo phương pháp tự hồi quy kết hợp trung bình trượt (ARIMA) để dự báo về giá bạc thế giới với dữ liệu trong giai đoạn 2021-2024 bằng phần mềm Stata. Đồng thời nghiên cứu cũng thực hiện so sánh kết quả dự báo theo mô hình ARIMA với mô hình Holt-winters và mô hình GARCH để đưa ra kết luận về mô hình nào phù hợp hơn cả khi thực hiện dự báo giá bạc thế giới (Nghiên cứu sử dụng cách viết số thập phân theo chuẩn quốc tế).
KẾT QUẢ NGHIÊN CỨU VÀ THẢO LUẬN
Thống kê mô tả dữ liệu
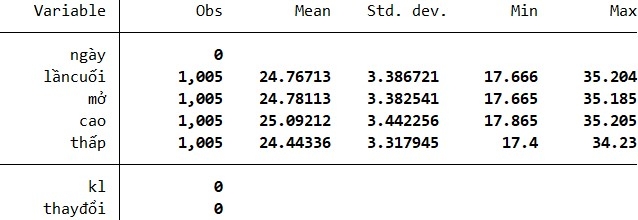
Bảng 1: Kết quả thống kê mô tả dữ liệu giá bạc
 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Kết quả Bảng 1 cho thấy, dữ liệu bao gồm 1.005 quan sát, mỗi quan sát đại diện cho một ngày giao dịch hợp đồng tương lai bạc. Trong đó:
- Giá đóng cửa chủ yếu tập trung quanh mức $24- $26.
- Giá mở cửa không khác biệt nhiều so với giá đóng cửa, cho thấy thị trường có xu hướng tiếp tục giá của ngày hôm trước.
- Giá cao nhất thường vượt trung bình một chút so với giá mở cửa và giá đóng cửa.
- Giá thấp nhất trong ngày thường nằm gần mức giá mở cửa, cho thấy sự ổn định nhất định.
Giá bạc dao động trong khoảng $17,666-$35,204, với mức trung bình gần $24,767.
Xây dựng mô hình ARIMA
Kiểm định tính dừng của chuỗi dữ liệu
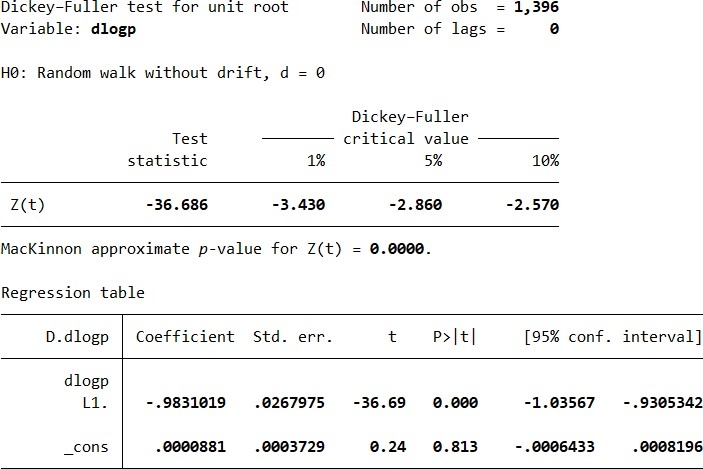
Bảng 2: Kết quả kiểm định ADF
 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Kết quả kiểm định ADF được cung cấp (Bảng 2) cho thấy giá trị thống kê Z(t) = -36.686, nhỏ hơn các giá trị tới hạn ở mức ý nghĩa 1%, 5% và 10%. Giá trị p-value = 0.0000, nhỏ hơn rất nhiều so với mức ý nghĩa 0.05. Điều này cho phép bác bỏ giả thuyết H0 (chuỗi thời gian là không dừng) ở mức ý nghĩa 1%. Kết quả kiểm định ADF cho thấy chuỗi thời gian dlogp là dừng. Hệ số của dlogp (L1.) = -0.9831019, cho thấy mối quan hệ nghịch biến giữa giá trị hiện tại và giá trị quá khứ của chuỗi đã được sai phân.
Hằng số (_cons) có giá trị 0.0000881 và p-value = 0.813, cho thấy không có xu hướng đáng kể trong chuỗi đã được sai phân.
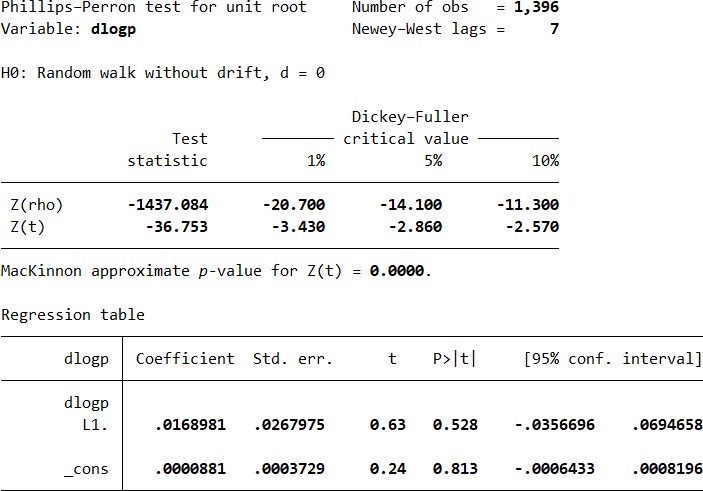
Bảng 3: Kết quả kiểm định Perron Phillips
 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Hình 3 cho thấy, giá trị Z(t) = -36.753 nhỏ hơn rất nhiều so với các giá trị tới hạn ở mức ý nghĩa 1% (-3.430), 5% (-2.860) và 10% (-2.570). Giá trị p-value = 0.0000, nhỏ hơn đáng kể so với bất kỳ mức ý nghĩa thông thường. Điều này cho phép bác bỏ giả thuyết H0 cho rằng chuỗi thời gian dlogp là không dừng. Hệ số của dlogp (L1.) = 0.0168981 và p-value = 0.528, có thể do chuỗi đã được sai phân trước đó để đạt tính dừng. Hằng số (_cons) = 0.0000881 và p-value = 0.813, cho thấy không có xu hướng đáng kể trong chuỗi đã được sai phân.
Tóm lại, kết quả kiểm định cho thấy chuỗi dlogp là dừng, phù hợp cho việc sử dụng trong các mô hình chuỗi thời gian.
Nhận dạng mô hình
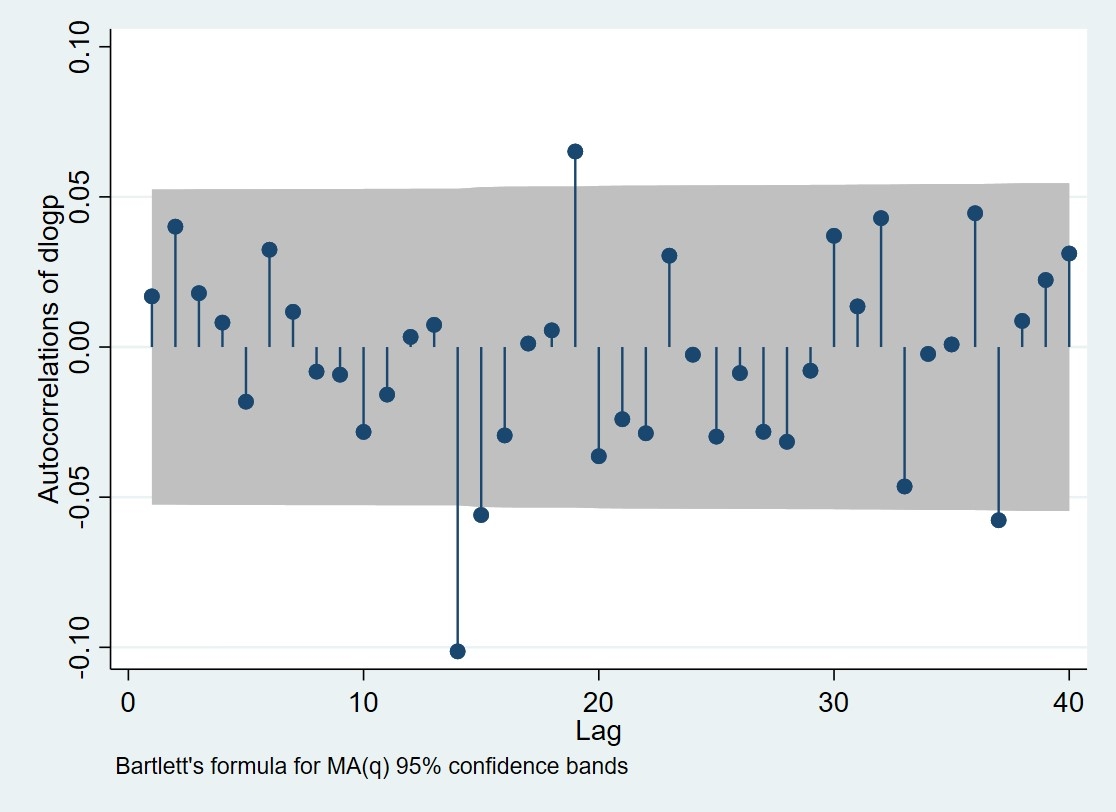
Hình 1: Biểu đồ ACF cho dữ liệu giá bạc
 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Hình 1 cho thấy, phần lớn các thanh tương quan đều nằm trong khoảng tin cậy, đặc biệt là ở độ trễ khoảng 14. Sau khi đã được sai phân (dlogp), chuỗi thời gian đã trở nên khá gần với một chuỗi ngẫu nhiên (white noise), hoặc ít nhất là không có tự tương quan mạnh mẽ ở các độ trễ lớn. Do đó, nếu sử dụng mô hình ARIMA, thì bậc MA(q) có thể được xem xét với các giá trị xung quanh các độ trễ có tương quan vượt ngưỡng hoặc có thể được bỏ qua nếu coi các tương quan này là do nhiễu ngẫu nhiên.
Hình 2: Biểu đồ PACF cho dữ liệu giá bạc
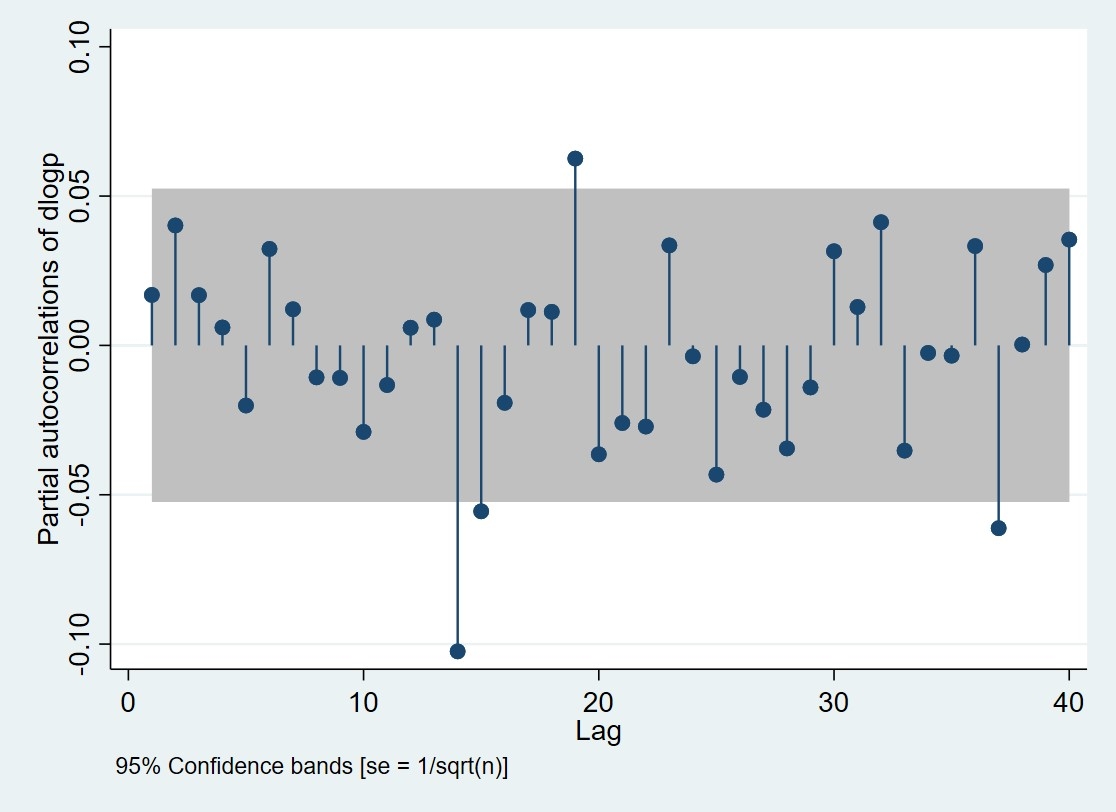 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Hình 2 cho thấy, hầu hết các thanh tương quan đều nằm trong khoảng tin cậy, cho thấy tương quan riêng phần ở các độ trễ này không đáng kể về mặt thống kê. Tuy nhiên, có một số điểm vượt ra ngoài khoảng tin cậy, đặc biệt là ở độ trễ khoảng 14, tương tự như hình kiểm định ACF.
Cả ACF và PACF đều có các điểm vượt ngưỡng ở cùng độ trễ cho thấy sự phức tạp trong cấu trúc tương quan của chuỗi thời gian và việc lựa chọn mô hình ARIMA phù hợp có thể cần nhiều thử nghiệm và đánh giá.
Ước lượng và kiểm định mô hình
Bảng 4: Kết quả kiểm định ADF kiểm tra phần dư có tính dừng cho mô hình ARIMA
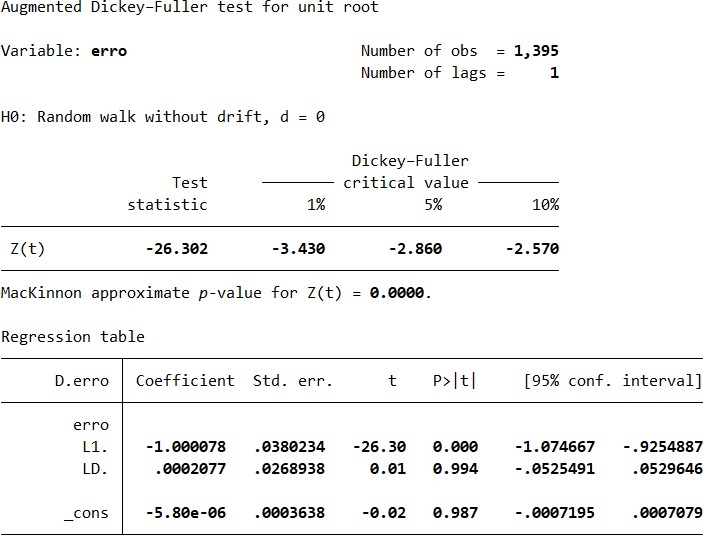 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Kết quả Bảng 4 cho thấy giá trị thống kê Z(t) = -26.302, nhỏ hơn so với các giá trị tới hạn ở mức ý nghĩa 1% , 5% và 10%. Giá trị p-value = 0.0000 cho thấy có thể bác bỏ giả thuyết H0, và phần dư có nghiệm đơn vị (tức là không dừng). Vậy phần dư của mô hình là dừng. Việc phần dư dừng cho thấy mô hình ARIMA đã được xây dựng phù hợp. Bảng hồi quy cho thấy hệ số của erro (L1.) = -1.000078 với p-value = 0.000, cho thấy mối quan hệ nghịch biến mạnh mẽ và có ý nghĩa thống kê giữa giá trị hiện tại và giá trị quá khứ của phần dư. Hệ số này rất gần với -1, cho thấy phần dư đã được sai phân hiệu quả để trở nên dừng. Các hệ số LD. và _cons đều không có ý nghĩa thống kê (p-value lần lượt là 0.994 và 0.987), cho thấy không có xu hướng hoặc tự tương quan đáng kể nào còn lại trong phần dư sau khi mô hình đã được áp dụng. Tóm lại, kết quả kiểm định ADF cho thấy phần dư của mô hình ARIMA là dừng, đáp ứng một trong những điều kiện quan trọng để mô hình được coi là phù hợp.
Kiểm định tính ổn định cấu trúc của mô hình
Hình 3: Kiểm định tính ổn định và khả nghịch cho mô hình ARIMA
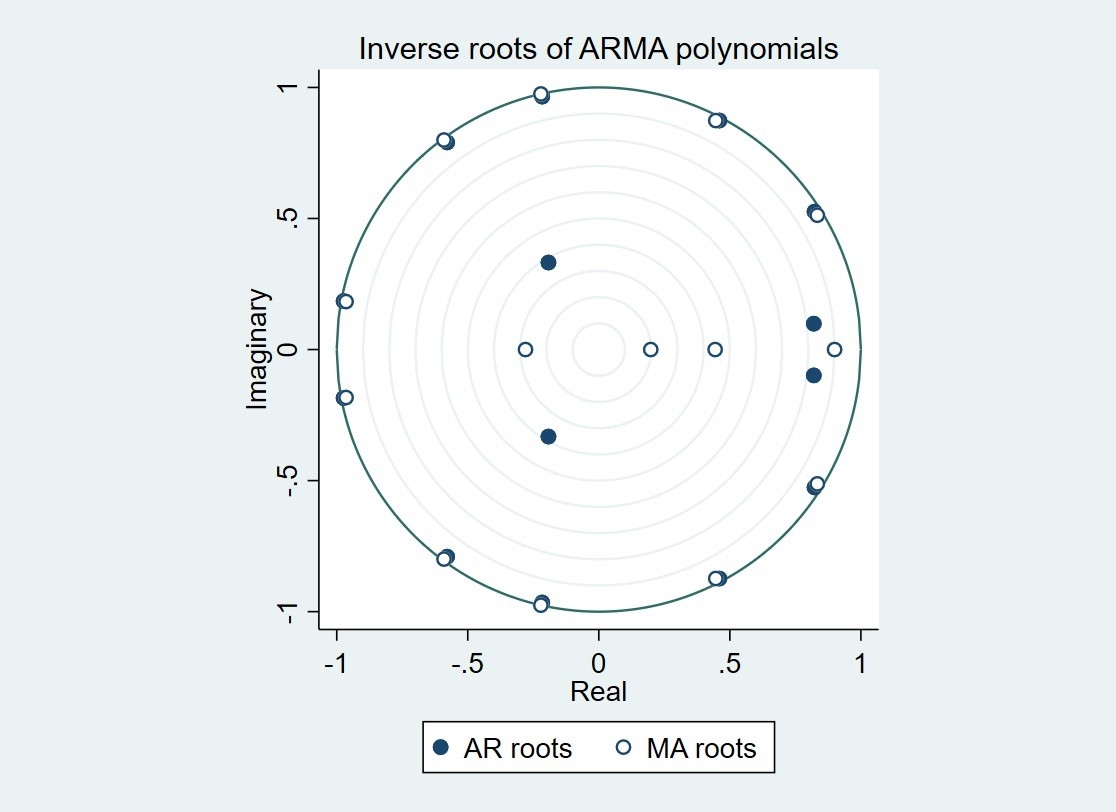 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Hình 3 cho thấy, mô hình ARIMA thỏa mãn cả điều kiện ổn định và điều kiện khả nghịch, nên mô hình được coi là hợp lệ để phân tích dự báo.
Đánh giá độ chính xác của mô hình dự báo
Bảng 5: Đánh giá hiệu suất mô hình ARIMA
| MAE | RMSE |
| 0.0094 | 0.0131 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Với MAE = 0.0094 và RMSE = 0.0131 (Bảng 5), ARIMA được đánh giá là có hiệu suất dự báo rất tốt, với sai số thấp và không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ.
Kết quả dự báo xu hướng giá bạc thế giới
Hình 4: Giá trị thực tế và giá trị dự báo của giá bạc sử dụng mô hình ARIMA
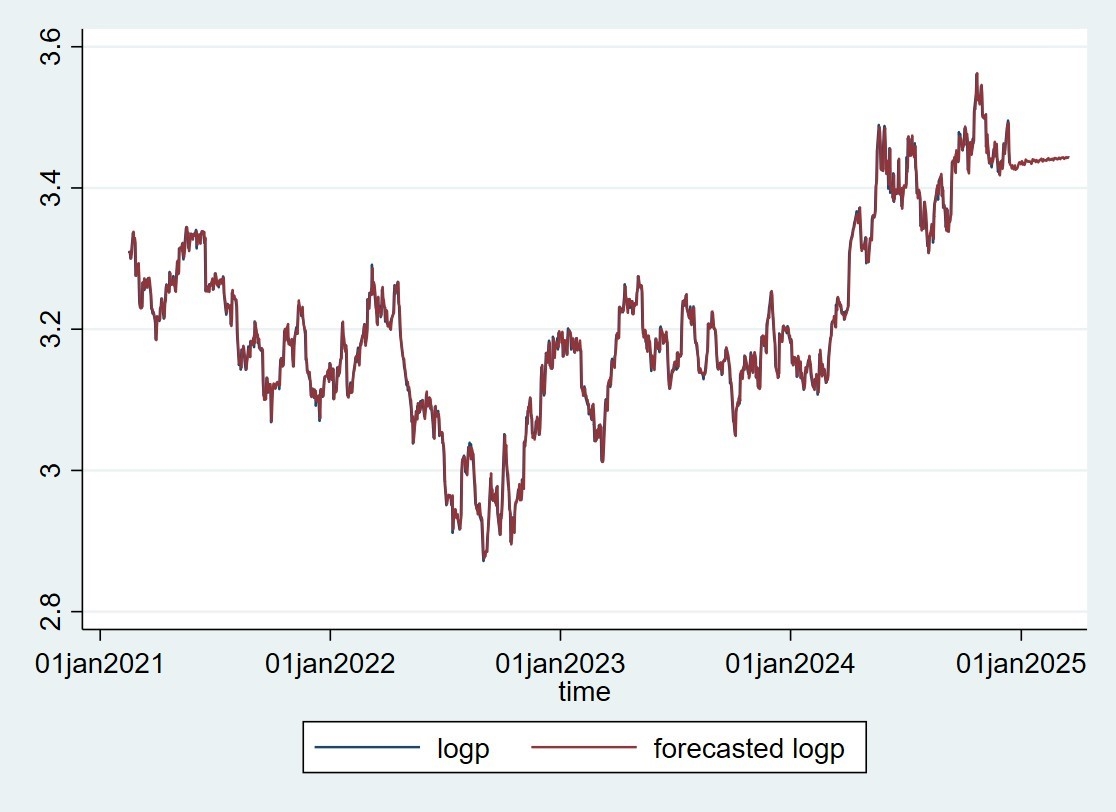 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Hình 4 cho thấy, từ đầu năm 2021 đến khoảng giữa năm 2023, 2 đường khá trùng khớp, cho thấy mô hình ARIMA đã dự báo tương đối chính xác diễn biến giá bạc. Tuy nhiên, từ giữa năm 2023 đến đầu năm 2025, có thể thấy một số khác biệt giữa giá trị thực tế và giá trị dự báo. Dù vậy, xu hướng chung của giá bạc vẫn được coi là dự báo tương đối chính xác. Giai đoạn dự báo từ đầu năm 2024 đến đầu năm 2025 cho thấy mô hình dự báo giá bạc ổn định hơn, với xu hướng đi ngang hoặc biến động nhẹ.
So sánh mô hình ARIMA với một số mô hình khác
Mô hình san mũ Holt -Winters
Bảng 6: Tham số trong mô hình san mũ Holt-Winters
 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Bảng 6 với giá trị alpha = 1 cho thấy mô hình phản ứng rất nhanh với những thay đổi gần đây trong dữ liệu. Giá trị beta rất nhỏ (0.0003) cho thấy mô hình ít chú trọng đến việc điều chỉnh xu hướng. Giá trị gamma » 1 (0.9999) cho thấy mô hình đặt trọng số rất cao vào thành phần mùa vụ. Điều này chỉ ra các mẫu mùa vụ gần đây sẽ lặp lại trong tương lai. “Penalized sum-of-squared residuals” và “sum-of-squared residuals” đều = 0.2745827 cho thấy không có thành phần mùa vụ được điều chỉnh. RMSE cho thấy độ chính xác của mô hình khá cao, với sai số dự báo trung bình là 0.0140147.
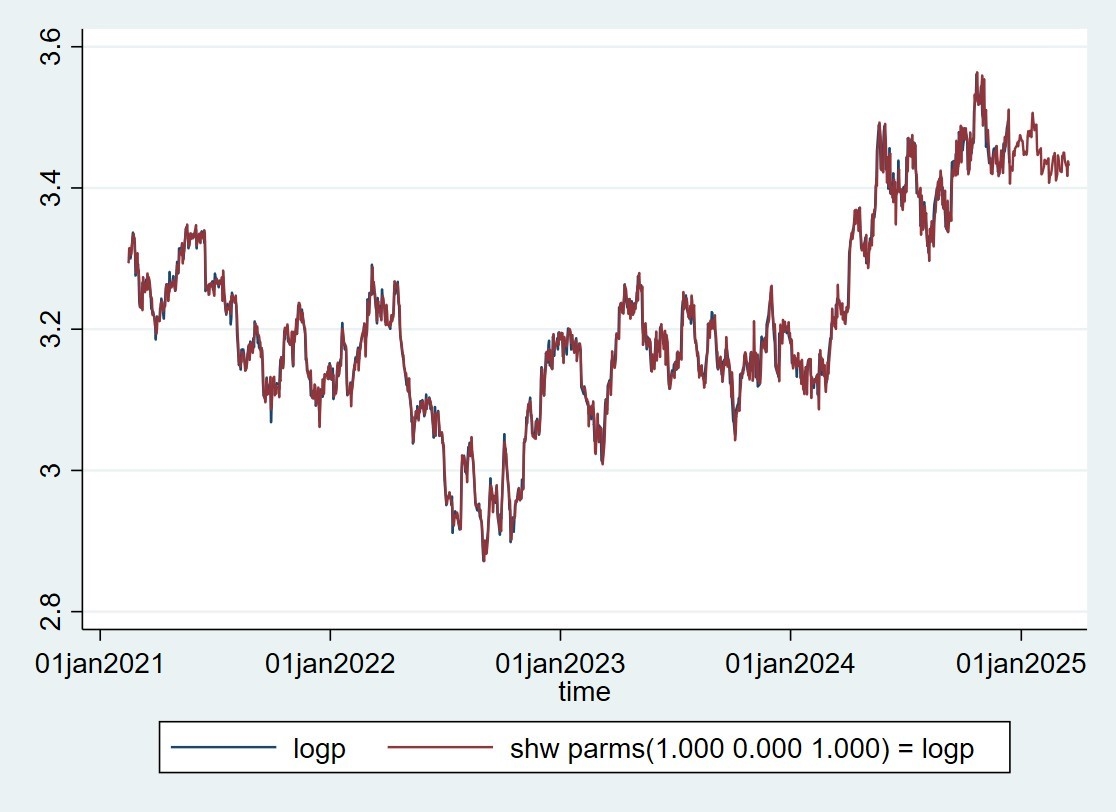
Hình 5: Giá trị thực và dự báo của giá bạc - mô hình san mũ Holt-Winters
 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Hình 5 cho thấy, đường giá trị thực tế và giá trị dự báo khá gần nhau, đặc biệt là trong giai đoạn từ đầu năm 2021 đến khoảng giữa năm 2023 và từ cuối năm 2024 đến đầu năm 2025. Điều này cho thấy mô hình Holt-Winters đã dự báo khá chính xác diễn biến giá bạc trong những giai đoạn này.
Việc các tham số của mô hình được hiển thị là (1.000 0.000 1.000) cho thấy alpha (mức độ) và gamma (mùa vụ) được đặt ở giá trị tối đa, trong khi beta (xu hướng) = 0. Điều này hàm ý rằng, mô hình tập trung hoàn toàn vào mức độ hiện tại và thành phần mùa vụ, bỏ qua xu hướng. Điều này có thể là một trong những nguyên nhân khiến mô hình gặp khó khăn trong việc dự báo các biến động mạnh. Tóm lại, biểu đồ cho thấy mô hình Holt-Winters đã thể hiện khả năng dự báo khá tốt cho giá bạc trong những giai đoạn ổn định, nhưng gặp khó khăn trong việc dự báo các biến động mạnh.
Mô hình GARCH
Bảng 7: Kết quả mô hình GARCH cho dữ liệu giá bạc
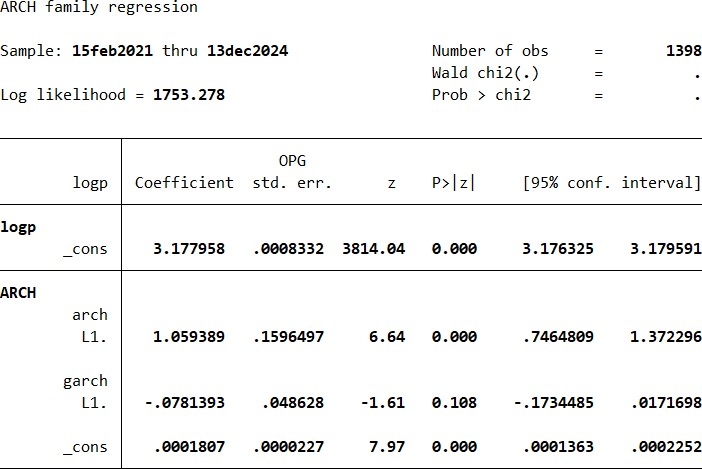 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
Kết quả Bảng 7 với hằng số (_cons) = 3.177958, độ lệch chuẩn (std. err.) = 0.0008332; giá trị z = 3814.04 và p-value (P > |z|) = 0.000, cho thấy hằng số này có ý nghĩa thống kê cao. Điều này đơn giản chỉ cho biết giá trị trung bình của logp = 3.177958. Hơn nữa, kết quả của phương trình phương sai được biểu diễn dưới phần “ARCH”. Cụ thể:
arch L1.: Hệ số của độ trễ bậc 1 của phần dư bình phương = 1.059389 với độ lệch chuẩn = 0.1596497. Giá trị z = 6.64 và p-value = 0.000, cho thấy hệ số này có ý nghĩa thống kê cao. Như vậy, có sự tự tương quan trong phương sai của giá bạc.
garch L1.: Hệ số của độ trễ bậc 1 của phương sai có điều kiện = -0.0781393 với độ lệch chuẩn = 0.048628. Giá trị z = -1.61 và p- value = 0.108, cho thấy hệ số này không có ý nghĩa thống kê ở mức ý nghĩa 5% hoặc 10%. Điều này cho thấy ảnh hưởng của phương sai có điều kiện trễ một kỳ lên phương sai hiện tại là không đáng kể.
_cons: Hệ số hằng số trong phương trình phương sai = 0.0001807 với độ lệch chuẩn = 0.0000227. Giá trị z = 7.97 và p-value = 0.000, cho thấy hệ số này có ý nghĩa thống kê cao. Điều này cho biết mức độ biến động cơ bản của giá bạc.
Giá trị “Log likelihood” = 1753.278, cho thấy giá trị của hàm hợp lý tại các ước lượng tham số. Giá trị này được sử dụng để so sánh các mô hình khác nhau.
Kết quả cho thấy có bằng chứng mạnh mẽ về hiệu ứng ARCH (tự tương quan trong phương sai) trong dữ liệu giá bạc, được thể hiện qua hệ số arch L1. có ý nghĩa thống kê cao. Tuy nhiên, hiệu ứng GARCH dường như không đáng kể trong mô hình này.
Bảng 8: So sánh hiệu suất của các mô hình
| Mô hình | MAE | RMSE |
| ARIMA | 0.0094 | 0.0131 |
| San mũ Holt-Winters | 0.0098 | 0.0136 |
| GARCH | 0.1019 | 0.1356 |
Nguồn: Nhóm tác giả tổng hợp, phân tích từ kết quả nghiên cứu
So sánh giữa 3 mô hình (Bảng 8) cho thấy mô hình ARIMA cho kết quả tốt nhất với MAE = 0.0094 và RMSE = 0.0131. Điều này cho thấy trung bình, các dự đoán của mô hình ARIMA lệch khoảng 0.0094 đơn vị so với giá trị thực tế và sai số bình phương gốc trung bình là 0.0131. Mô hình San mũ Holt-Winters có hiệu suất kém hơn một chút so với ARIMA, với MAE = 0.0098 và RMSE = 0.0136. Sự khác biệt này không quá lớn, cho thấy cả 2 mô hình ARIMA và Holt-Winters đều có khả năng dự báo khá tốt cho dữ liệu giá bạc. Tuy nhiên, mô hình GARCH cho kết quả với MAE = 0.1019 và RMSE = 0.1356. Các giá trị này lớn hơn đáng kể so với 2 mô hình còn lại, cho thấy mô hình GARCH dự báo kém chính xác hơn nhiều.
KẾT LUẬN
Kết quả nghiên cứu chỉ ra rằng, mô hình ARIMA thể hiện khả năng dự báo giá trị trung bình tốt nhất, tiếp theo là mô hình san mũ Holt-Winters. Mô hình GARCH, tập trung vào biến động, không phù hợp cho việc dự báo trực tiếp giá trị nhưng hữu ích cho việc đánh giá rủi ro. Do vậy, trong những mô hình trên, nên ưu tiên sử dụng mô hình ARIMA cho dự báo giá bạc, kết hợp với mô hình san mũ Holt-Winters để so sánh và xem xét yếu tố mùa vụ (nếu có). Hạn chế sử dụng GARCH cho mục đích dự báo giá trị trung bình. Hơn nữa, để đưa ra quyết định đầu tư sáng suốt, cần phải kết hợp kết quả dự báo với các phân tích khác, cập nhật mô hình thường xuyên, hiểu rõ hạn chế của mô hình và xem xét trong bối cảnh kinh tế cụ thể.
Tài liệu tham khảo:
1. Alomoto, W., Niñerola, A., & Pié, L. (2021). Social Impact Assessment: A Systematic Review of Literature, Social Indicators Research, 161, 225-250.
2. Box, G. E. P, Jenkins, G. M. (1976). Time series analysis forescasting and control, 1st edition, Wiley.
3. Chen, C., Hu, J., Meng, Q. & Zhang, Y. (2011). Short-time traffic flow prediction with ARIMA-GARCH model, IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany.
4. Clements, M. P., & Hendry, D. F. (2012). The Oxford Handbook of Economic Forecasting, Oxford University Press.
5. Fahimifard, S.M., Homayounifar, M. Sabouhi, M. And Moghaddamnia, A.R. (2009). Comparison of ANFIS, ANN, GARCH and ARIMA techniques to exchange rate forecasting, Journal of Applied Sciences, 9(20), 3641-3651.
6. Mazov, N. A., Gureev, V. N., & Glinskikh, V. N. (2021). The Methodological Basis of Defining Research Trends and Fronts, Scientific and Technical Information Processing, 47, 221-231.
7. Tan, Z., Zhang, J., Wang, J. & Xu, J. (2010). Day-ahead electricity price forecasting using wavelet transform combined with ARIMA and GARCH models, Applied Energy, 87, 3603-3610.
8. Thu Dung (2024). Giá bạc tăng gần 92% trong 5 năm qua, https://thoibaotaichinhvietnam.vn/gia-bac-tang-gan-92-trong-5-nam-qua-162209.html.
| Ngày nhận bài: 20/9/2025; Ngày hoàn thiên biên tập: 14/10/2025; Ngày duyệt đăng: 22/10/2025 |

























Bình luận